Chapter 1: Introduction to the Beal Conjecture

Beyond the well-known Millennium Prize Problems, there are numerous other unresolved mathematical issues that could reward a million-dollar prize. This article delves into the Beal conjecture, its links to Fermat’s last theorem, and the advancements made thus far.

In 1993, Andrew Beal, a banker and amateur mathematician, proposed the following conjecture:

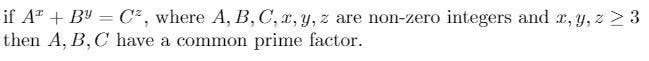
Beal Conjecture

Let's explore some examples to clarify this statement.

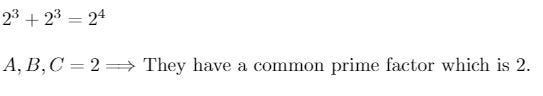
Consider A, B, C = 2 || x, y = 3 || z = 4. A slightly more complex example could be:

Here, A, B = 7 || C = 14 || x, z = 3 || y = 4.

Fermat’s Last Theorem

In approximately 1637, Pierre de Fermat conjectured that:

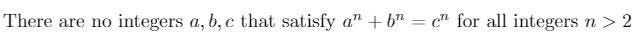
For nearly 30 years, this conjecture remained unresolved, gaining notoriety as one of the most challenging problems in mathematics. Before its proof in 1994, it was recorded in the Guinness Book of World Records as the "most difficult mathematical problem." While there is much more to discuss regarding Fermat’s last theorem, we will focus on its relevance to this article.

By applying Fermat’s last theorem to the Beal conjecture, we can conclude that when x = y = z, there are no integer solutions. This conclusion implies that if no such solution exists, then the Beal conjecture holds true in this scenario.

If you’re interested in exploring more about Fermat’s last theorem, I recently read "Fermat’s Last Theorem" by Simon Singh. It provides a historical context in an accessible manner, making it enjoyable for those without a deep mathematical background. You can find this book on Amazon. (Disclaimer — affiliate link)

What Do We Know So Far?

Although the Beal conjecture is relatively new compared to Fermat’s last theorem, significant partial results have emerged, with notable progress made as recently as 2014.

One of the most important partial results relates to the case:

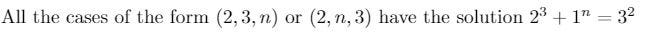
Here, (x, y, z) = (2, 3, n) or (2, n, 3). This case is known as the Catalan solution, and other solutions build upon it. For instance, in 2003, Nils Bruin demonstrated that for (x, y, z) = (2, 3, 8), there is only one non-Catalan solution, which does not contradict the Beal conjecture.

In 2014, researchers Bennett, Chen, Dahmen, and Yazdani proved that both cases (x, y, z) = (3, 6, n) where n > 2, and (x, y, z) = (4, 2n, 3) where n > 1 align with the Beal conjecture. For a comprehensive list of all partial results, refer to Wikipedia.

Final Thoughts

Currently, the reward for proving the Beal conjecture or providing a counterexample stands at $1,000,000. A quick online search revealed two proofs that have yet to be accepted: Nicholas J. Daras submitted his proof in March 2019, while Leandro Torres Di Gregorio submitted his proof in September 2013. More details about this prize can be found on the American Mathematical Society's website.

The first video explores how an MIT professor tackles a million-dollar math problem, shedding light on the complexities of the Beal conjecture.

The second video challenges viewers to solve a mathematics problem for a chance at one million dollars, further emphasizing the allure of the Beal conjecture.