Chapter 1: Introduction to the Sphere Puzzle

Consider this intriguing scenario: What if we attempt to fit three spheres, each with a radius of 1, into a cylinder that is just large enough to hold them? What can we deduce about the volume that remains unoccupied?

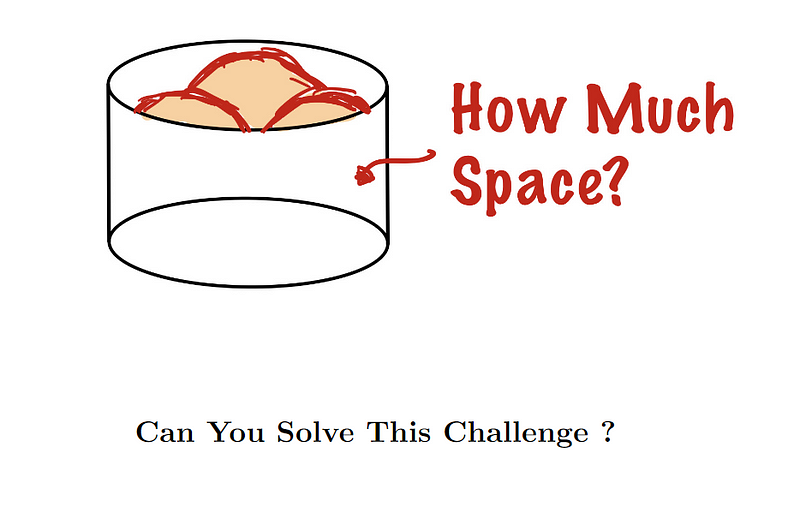
Question of the Day A hint for you: Connect the centers of the spheres and see what insights arise. Take a moment to pause, grab some paper, and engage with the problem. Once you’re ready, continue for the solution!

Solution Overview Before we delve into the mathematics, let’s visualize the setup. Each sphere rests on a surface, and the cylinder is just wide enough to encompass them, implying that every sphere must make contact with the other two. This configuration leads to the centers forming a triangle.

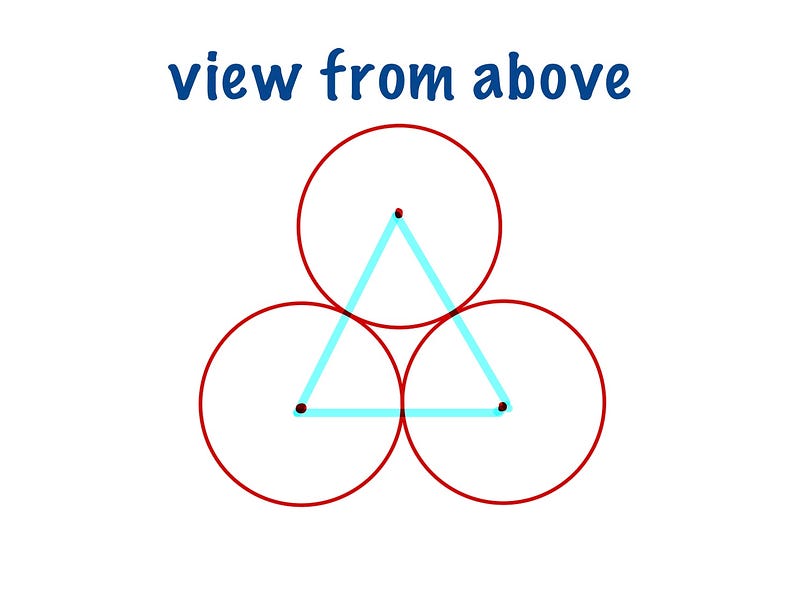
The image illustrates how three unit spheres are arranged. The cylinder surrounding them has a height of 2 units, and we can further annotate this diagram.

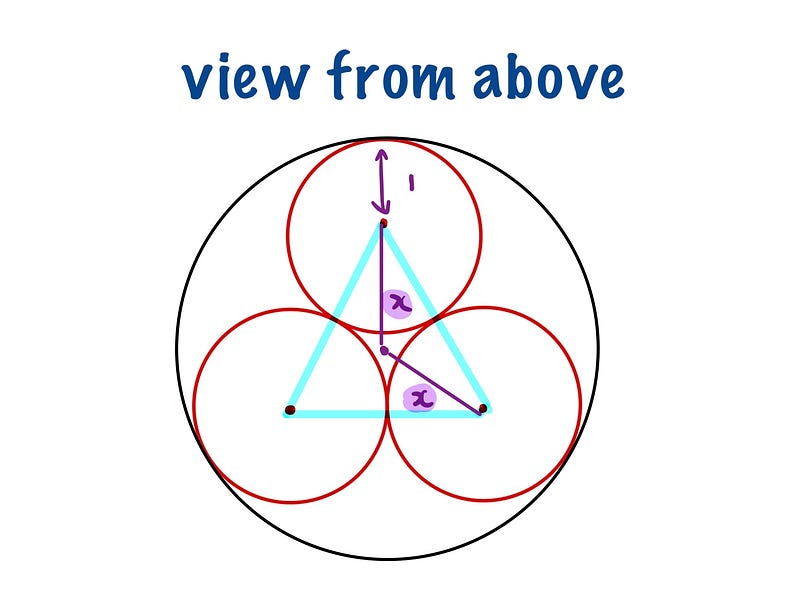
Here are the key details: - Each sphere has a radius of 1. - The distance from the center of each sphere to the center of the cylinder is denoted as x. - Consequently, the radius of the cylinder is 1 + x.

Next, we calculate the volume of the three spheres:

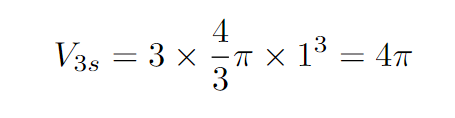
Our goal is to determine the value of x, which will enable us to compute the volume of the cylinder, allowing us to find out how much of the cylinder's interior is filled.

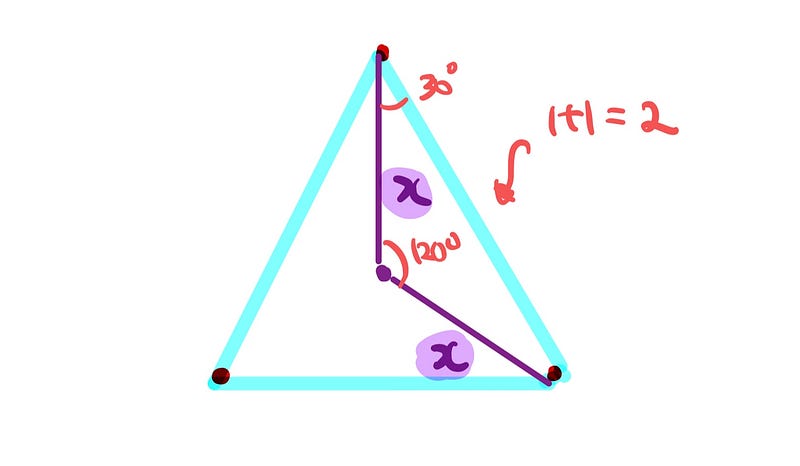
We will analyze the isosceles triangle formed, with sides of length x, x, and 2. The side length of 2 arises from the sum of the radii of the spheres. To find x, we can apply the sine rule.

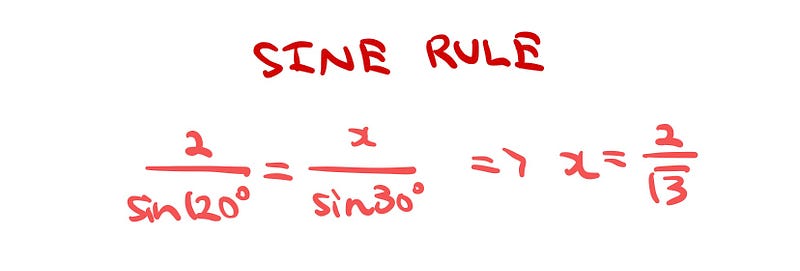
Thus, we can determine the radius of the cylinder as follows:

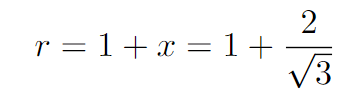
The cylinder's volume is calculated by multiplying the area of its base by its height:

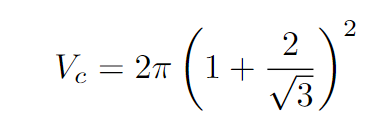
To arrive at our final answer, we will divide the combined volume of the spheres by the volume of the cylinder. Be sure to verify that your algebra is accurate!

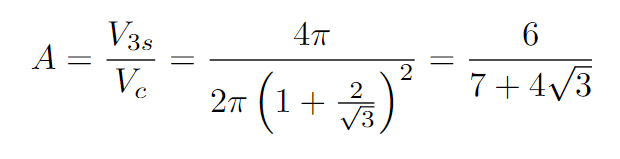
Fascinating, isn't it? And for a fun note, here's an adorable drawing of a leopard!

And that's how we arrive at our conclusion! What were your thoughts during this exercise? Please share in the comments—I’m curious to learn!

Chapter 2: Exploring Volume with Visual Aids

In this video, titled The available space occupied by spheres of equal size in three dimensions, we explore how these spheres interact within a confined space.

Another insightful video, Understanding the Volume of a Sphere Formula [Using High School Geometry], delves into the mathematical principles underlying sphere volume calculations.

Conclusion Thank you for engaging with this mathematical exploration! If you found this insightful, don’t hesitate to share and support more content like this.