Chapter 1: Understanding the Golden Ratio

The Golden Ratio, often referred to as the Divine Constant, is a captivating concept that appears in various branches of mathematics and science. It can be illustrated through a line segment divided into two parts, where the ratio of the total length to the larger segment equals the ratio of the larger segment to the smaller one. This ratio defines the Golden Ratio. A visual representation may clarify this concept:

Another common way to express the Golden Ratio is through a specific equation:

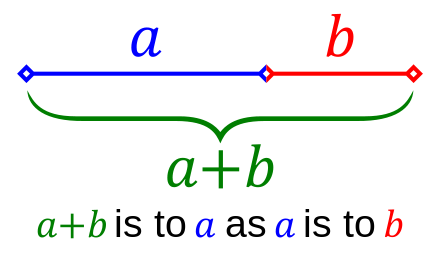
Through some algebraic manipulation using the quadratic formula, the Golden Ratio can be derived as (1 + √5)/2, an irrational number roughly equal to 1.618. There are multiple representations of this ratio, one of which involves the ratios of consecutive Fibonacci numbers. The Fibonacci sequence begins with 1 and 1, with each subsequent number being the sum of the two preceding numbers:

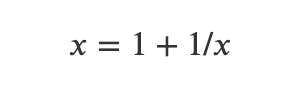
The initial terms of this sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and it becomes apparent that as the sequence extends, the ratio of each term to its predecessor converges to the Golden Ratio:

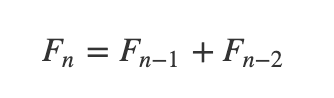
Recently, I encountered a challenging high school exam question that illustrated not only the emergence of the Golden Ratio from Fibonacci numbers but also how the Fibonacci sequence reappears when deriving the Golden Ratio through other methods. This discovery was quite intriguing.

The question posed was as follows:

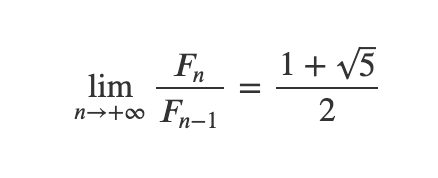
At first glance, it may not be clear how this question relates to the Golden Ratio or Fibonacci numbers. The problem presents a finite cyclical sequence of n terms, where each term is defined based on the next, culminating in a definition involving the first term.

First, let's address the question directly. This approach will lead us to the Golden Ratio without initially connecting to Fibonacci numbers.

Part (i) is straightforward. Since each term (x_i) is positive, it follows that (1/x_i > 0), hence (1 + 1/x_i > 1). Therefore, all terms must be greater than 1.

Part (ii) is also manageable. The following method demonstrates this clearly:

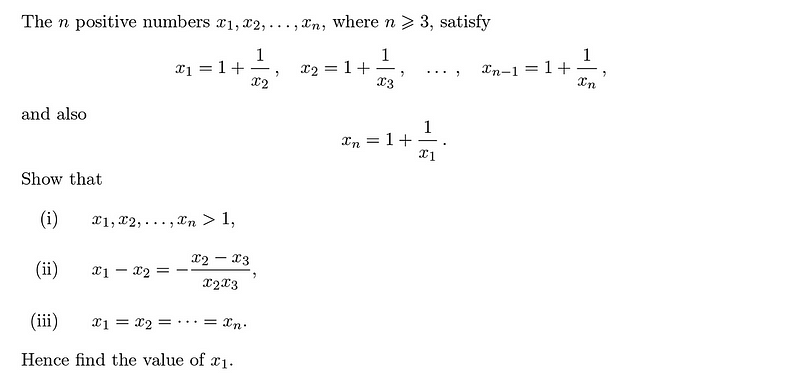
The most challenging aspect arises in part (iii), which can be resolved by applying the method from part (ii), observing that:

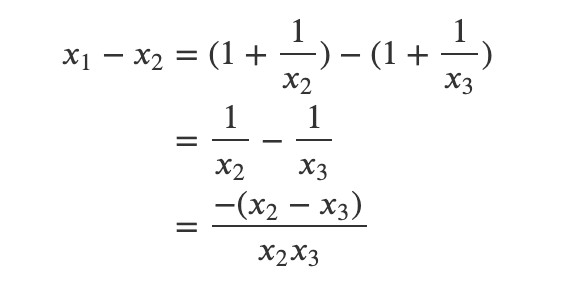
Eventually, utilizing the cyclic nature of the sequence will bring us back to:

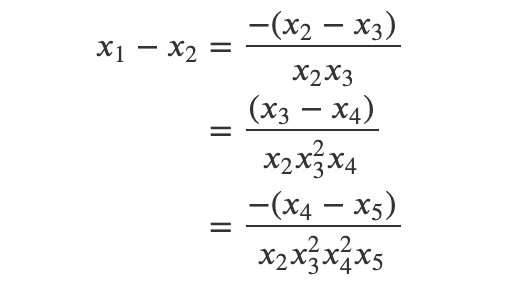
From this, we can conclude:

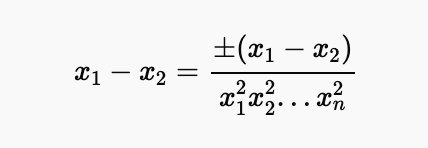
Given that all terms are strictly greater than 1, as established in part (i), the second factor cannot equal zero. Consequently, we find (x_1 = x_2), and this reasoning applies universally, confirming (x_1 = x_2 = ... = x_n).

To conclude this question, we determine that our entire sequence simplifies to the equation:

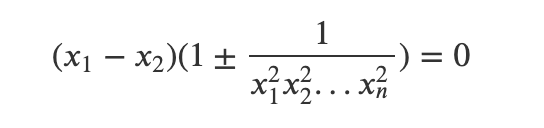
This equation has a solitary positive solution: the Golden Ratio (1 + √5)/2.

Chapter 2: An Alternate Perspective Involving Fibonacci Numbers

What if we approached this problem differently? By using the definitions of our sequence recursively, we can express (x_1) in terms of any following term, such as:

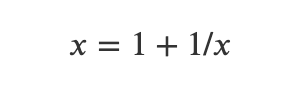
Continuing this recursive process yields:

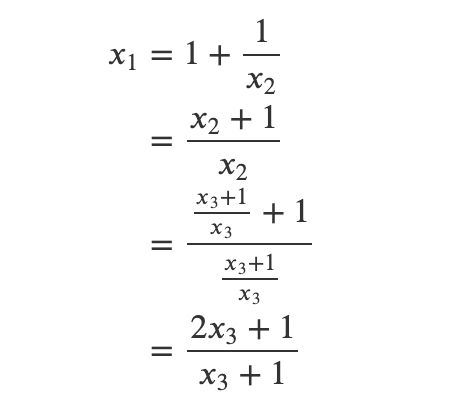
Do these coefficients look familiar? Indeed, they correspond to the Fibonacci numbers. Generally, we can express:

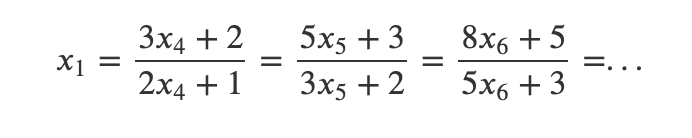
Although I won't provide a formal proof, it is straightforward to verify using induction and the characteristics of the Fibonacci sequence.

Considering the case where (k = n):

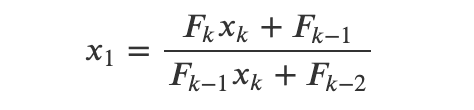
Rearranging gives us:

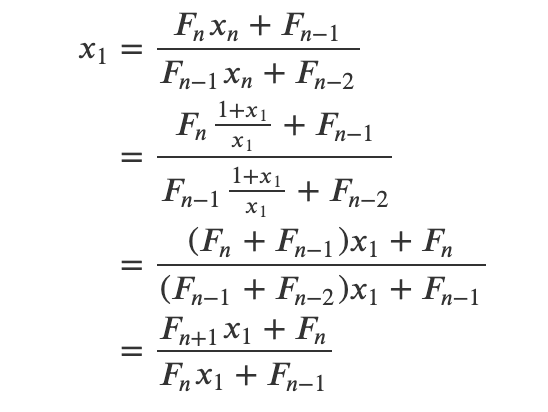
Utilizing Fibonacci properties simplifies this expression to:

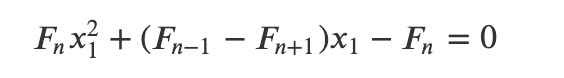
Dividing by (F_n) leads us back to our original quadratic equation related to the Golden Ratio.

It is truly captivating how such fundamental mathematical concepts are intricately linked. While I've always admired how Fibonacci numbers lead to the Golden Ratio, I find it particularly interesting that investigating the formula (x = 1 + 1/x) can also reveal Fibonacci numbers.

I hope you found this exploration enjoyable. Feel free to share your thoughts in the comments!

This video titled "The Golden Ratio and the Fibonacci Numbers" delves deeper into the fascinating relationship between these two mathematical concepts.

In this lecture, "Lecture 8 | Fibonacci Numbers and the Golden Ratio," viewers can enhance their understanding of these topics through comprehensive explanations and examples.