The Traditional Definition

The widely accepted definition of a derivative is given by the expression f(x+h) - f(x), divided by h:

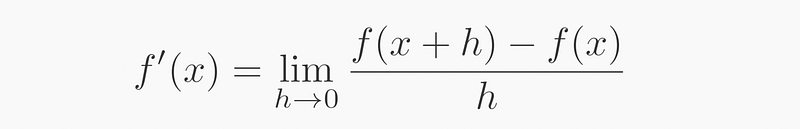
This formula clearly illustrates the subtraction between two points, representing the tangent of the angle of the triangle formed by these points.

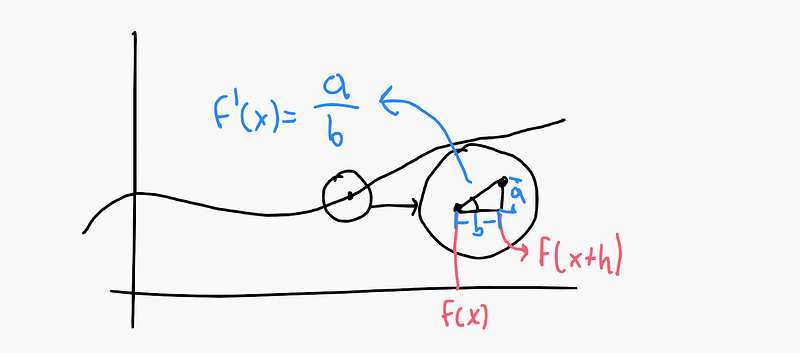
While this definition works effectively in one dimension with x and f(x), we must consider how it applies when we venture into complex analysis.

The Derivative in Complex Analysis

In complex analysis, we aim to incorporate the definition from real analysis, thereby expanding our understanding from real numbers to complex numbers.

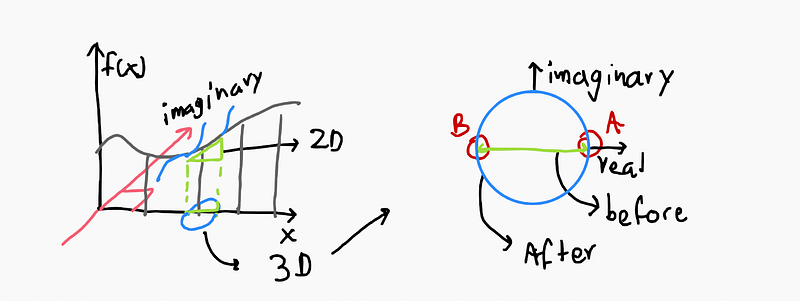
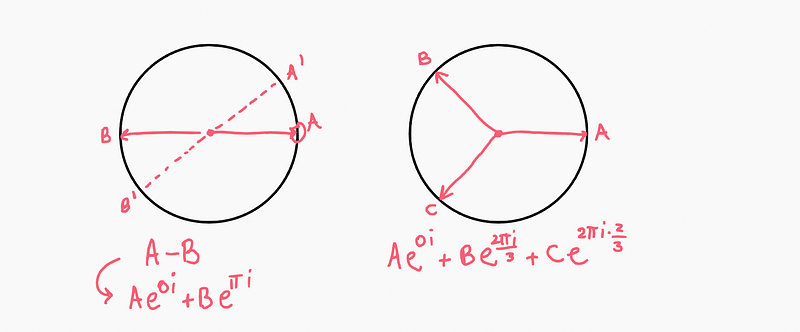
As depicted above, the derivative in real numbers is primarily concerned with the subtraction of two points (A) and (B). In complex analysis, however, we can conceptualize this as a contour where we are "subtracting" all points along that contour. The question arises: how can we subtract more than two points, distinguishing between positive and negative values?

The answer lies in recognizing that it was never truly a subtraction; it has always been a summation. Essentially, we are dealing with an integral or a dot product. Complex numbers behave similarly to vectors, with negative numbers interpreted as positive lengths rotated by 180°.

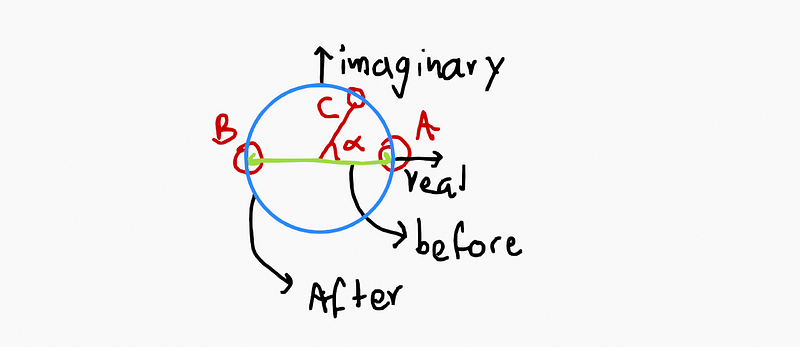
Consider this: we add point A at 0°, point B at 180° (which represents -1), and point C at an angle α. Here, the angle serves as a generalization of sign, with positive being 0° and negative being 180°. This framework allows us to navigate the previously “subtractive” behaviors of derivatives, as we now have a spectrum of angles to consider.

The Integral Perspective of Derivatives

I have recently discussed Cauchy’s integral formula (in its generalized form), which states:

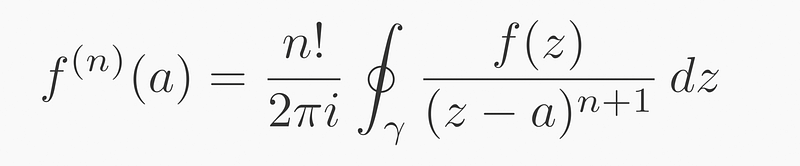
Prerequisites for Application

It's essential to note that Cauchy’s formula only applies to functions that satisfy specific criteria:

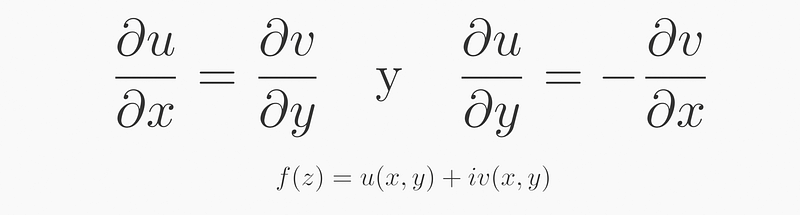
This implies that the derivative remains consistent regardless of the direction from which it is approached, ensuring a singular result for each point in the domain.

The First Derivative

The first derivative can be expressed as follows:

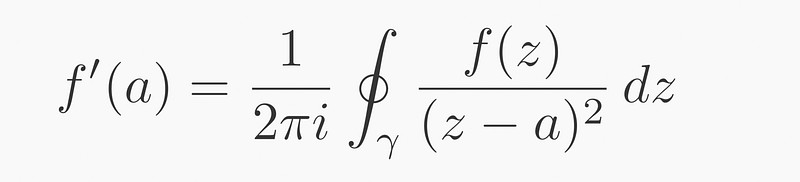
To understand how this captures the difference f(x+h) - f(x), we center our focus around the point a, allowing us to rewrite (z-a) as h*exp(i*angle). This is the phasor notation of a vector or complex number.

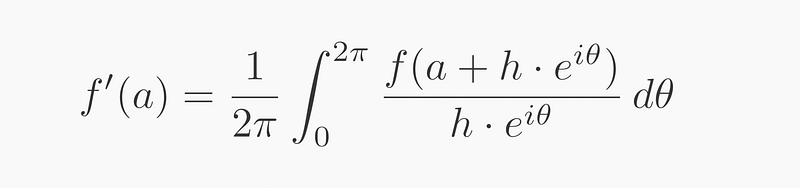
This formula simplifies down to a summation (integral) from angles 0 to 2π. By evaluating only at 0 and π, we revert to the original definition of the derivative, courtesy of Euler's identity exp(i*π) = -1 and exp(i*0) = 1.

For θ=0:

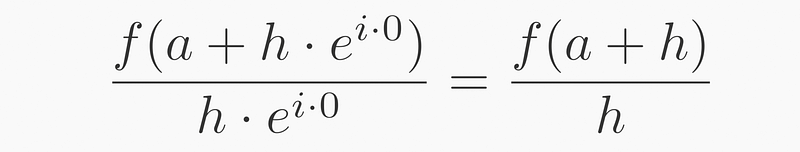
For θ=π:

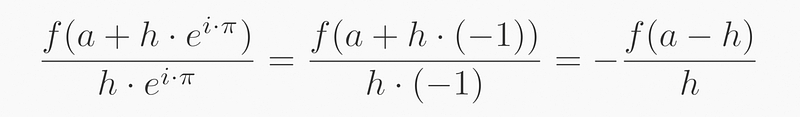
This summation, when simplified, leads us back to the original derivative definition:

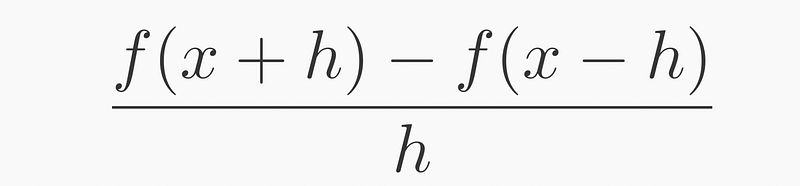
In essence, the Cauchy-Riemann conditions affirm that the derivative should yield the same result from all directions, ensuring that the subtraction remains equal across various angles.

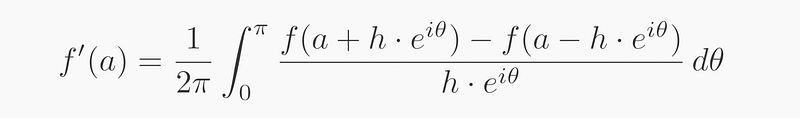
And indeed, Cauchy-Riemann conditions indicate that the derivative should be invariant across all directions, making the integration process yield a constant result.

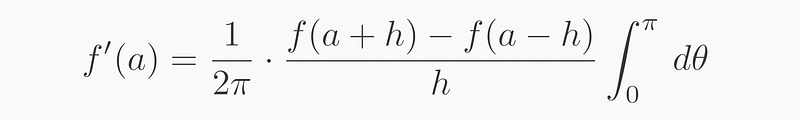
This results in the original definition of the derivative, ultimately leading to:

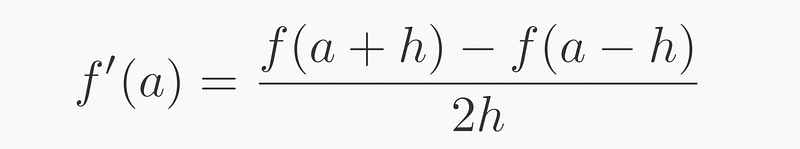
It's important to note that while the derivative may not be identical across all directions, it is influenced by exp(i*θ), which cancels out with the exponential in the denominator. This "rotation" aligns the derivative's angle to fit the plane in the real domain.

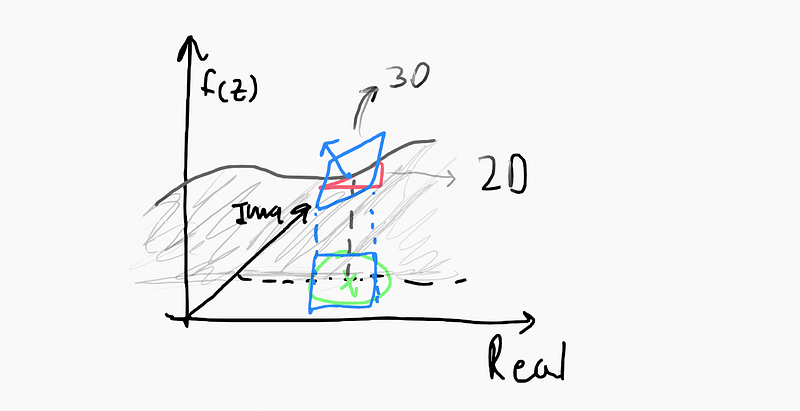
Transitioning the derivative from the real to the complex number domain transforms it from a linear segment to a plane that has an inclination. The Cauchy-Riemann conditions facilitate this process.

The Role of Contour Integrals

The contour integral essentially performs a dot product of f(exp(i*θ)) around a circumference, yielding insights about the tangent plane. While the initial derivative definition provides the tangent of the inclination, the extension into complex number domains reveals the inclination of the plane itself. The normal vector of this plane may be associated with the residue, but that exploration can be reserved for another discussion.

Higher Order Derivatives

The generalized Cauchy’s integral formula indicates that derivatives can be computed using closed integrals. This concept illustrates the transition from a subtraction-based approach to one that is fundamentally integral in nature, where the minus sign from subtraction reflects the phasor rotating by π (180°).

While delving deeply into this topic could be lengthy, the primary concept explaining why this extension holds has been articulated for the first derivative.

To visualize this further, consider:

The first video titled "The Derivative of an Integral" explores these integral concepts in depth, providing an engaging visual representation.

Further Insights into Derivatives

Complex analysis offers an intuitive approach to understanding derivatives, particularly when addressing higher-order derivatives. The second derivative, for instance, is influenced by the squared term (z-a)², prompting interesting interpretations.

In this context, the second derivative involves a subtraction of two opposing phasors, while the third derivative introduces a more complex interplay of phasors that we interpret directly without relying on subtraction.

In closing, the connection between these concepts and generating functions highlights an intriguing parallel.

The second video, "Derivative vs. Integral: Final Smackdown!" delves into the contrasting aspects of these mathematical concepts, offering insightful perspectives.

Incorporating these ideas into practical applications, such as image processing, allows us to apply the derivative in a two-dimensional space (complex numbers). This redundancy in deriving values across various angles aids in noise reduction and extends the kernel size for image analysis.

Thank you for your attention!