Exploring Fractional Derivatives: A Deep Dive into Mathematics
Written on
Understanding the Concept of Fractional Derivatives
In traditional education, we learn about derivatives defined by whole numbers. For instance, the first derivative of e²x is simply 2e²x. If we differentiate once more, we arrive at 4e²x. Up until this point, we are taking the derivative a whole number of times. However, what does it imply to take a derivative 0.5 times, or even n times? This article aims to shed light on that very question.
Let’s start with the function x² to keep things straightforward. Differentiating this yields 2x; this is achieved by lowering the exponent and reducing it by one. If we apply this process to x^n, we obtain nx^(n-1). By repeating this operation n times, we derive n(n-1)...2x, where the coefficient corresponds to the factorial function n!.
While it may seem unrelated, this concept is quite beneficial. Now, let’s consider the 0.5th derivative of x^(0.5). Based on our previous insights, we find that this equates to (0.5)!. A factorial of a non-integer? That sounds strange! However, it’s possible to extend the factorial function not only to positive rational numbers but further still. In fact, we can expand this concept to complex numbers, excluding non-positive integers! This extension is known as the Gamma function, which is represented as follows:
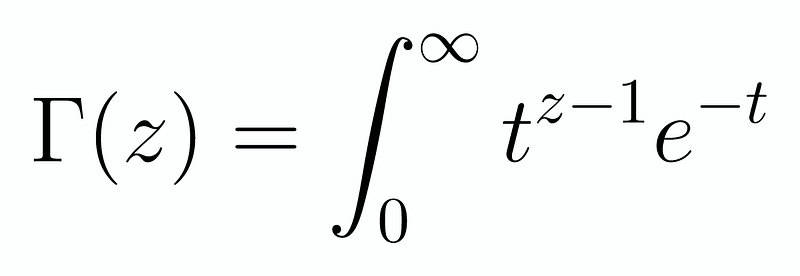
At first glance, this might seem arbitrary, yet if you substitute any positive integer, you will find that Γ(z-1) = z!. This enables us to extend factorial calculations beyond positive integers! Next, we examine something remarkable: Euler’s reflection formula:
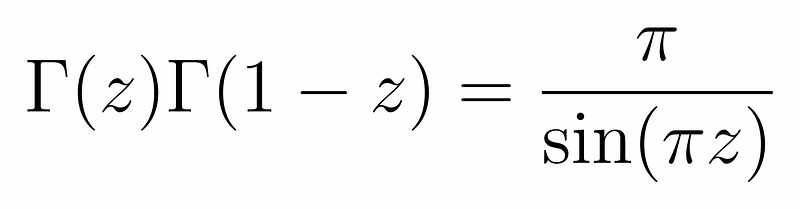
Initially, this may not appear practical, but it indeed has utility. If we set z = 1/2, we derive that Γ(1/2)² = π/sin(π/2) = π. Since the Gamma function is always positive for real values, we conclude that Γ(1/2) = √π. Returning to our earlier question, what is the 0.5th derivative of x^(0.5)? This corresponds to (1/2)!, which ultimately leads us to Γ(3/2). The relationship Γ(n) = nΓ(n-1) can be easily verified, and readers are encouraged to explore its validity! Consequently, we discover that Γ(3/2) = Γ(1/2)/2 = √π/2, indicating that the 0.5th derivative of x^(0.5) is indeed √π/2.
Extending Our Understanding
But we can delve even deeper! What is the n-th derivative of x^n? This simplifies to Γ(n+1). Unfortunately, this does not yield a straightforward representation and is not even elementary! However, we shouldn’t always anticipate a neat solution. For reassurance, the approximate value of this expression is 7.188.
Now, what additional insights can we gain from these fractional derivatives? Let’s examine e^(ax). The first derivative results in ae^(ax), the second yields a²e^(ax), and so on. Thus, we can generalize this to state that the n-th derivative is a^n e^(ax). Continuing this pattern, we can also express the fractional derivative as a^(1/2) e^(ax).
While this article could continue to explore further aspects, I believe it’s essential for readers to engage with this topic independently and discover the exciting possibilities it offers.
The first video titled "How to Find a Formula for the nth Derivative of f(x) = e^(kx)" provides a practical explanation of these concepts.
The second video titled "Formula for the nth Derivative of f(x) = 1/x" dives deeper into the formulaic approaches to derivatives, enhancing your understanding of the topic.