Exploring Fractal Structures in Bach's Cello Suite No. 3
Written on
Chapter 1: The Musical Genius of Bach
Johann Sebastian Bach is celebrated for his remarkable ability to blend artistic expression with mathematically inspired musical constructs. While his compositions may not strictly adhere to what we define today as "algorithmic," the organization of the phrases in the opening section of the first Bourrée from his Cello Suite No. 3 reveals an inherent hierarchical structure. This arrangement demonstrates a measurable power-law relation and can be interpreted through a fractal lens.
Musical phrasing mirrors linguistic structures, as both deal with the natural associations between sequences. This specific composition can be broken down into phrases that follow an AAB format, where the duration of each A segment is relatively short compared to the B segment, which is twice as lengthy. The first 16 measures of this piece (with the first eight measures repeated) are illustrated in Figure 1, showcasing the phrase groupings with horizontal braces.

Figure 1: Analysis of the first 16 measures of the Bourrée from Suite No. 3.
The initial beat of the piece initiates a phrase, m1, characterized by a double eighth note pickup followed by a quarter note. The pattern for phrase m1 can be described as:
Short (1 quarter beat) Short (1 quarter beat) Long (1 half beat).
This description also applies to the subsequent phrase, m2. Figure 2 provides a graphical depiction of these “Level 1” phrases, where blue notes represent short elements, red notes indicate long elements, and gray notes are not relevant. The x-axis illustrates time while the y-axis indicates pitch.

Figure 2: A graphical representation of the Level 1 phrases for the first eight measures (with pickup).
Referring back to Figure 1, phrases m1 and m2 serve as one-beat tonic phrases that lead into the two-beat dominant phrase, m3. Collectively, m1, m2, and m3 constitute the antecedent, s1, which follows the pattern:
Short (1 beat) Short (1 beat) Long (2 beats).
The concluding half beat of measure 2 introduces a diatonic transposition of m1, denoted as m1?, followed by a diatonic transposition of m2, labeled m2?. These two tonic phrases (the second pair of three-note phrases in Figure 2) are succeeded by the two-beat tonic variation of m3, termed m3v?, completing the consequent, s2. Figure 3 illustrates these “Level 2” phrases.

Figure 3: Graph of the Level 2 phrases.
The initial eight beats can thus be segmented into two four-beat subjects, s1 and s2, which precede an extended eight-beat continuation, s3. When combined, s1, s2, and s3 reveal the overarching structure:
Short (4 beats) Short (4 beats) Long (8 beats).
Figure 4 visualizes these “Level 3” phrases.
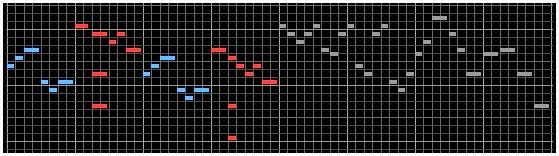
Figure 4: Graph of the Level 3 phrases.
This analysis indicates a recursive series of scaled phrases following the AAB format. Notably, the first eight measures repeat, creating two “short” sections that lead into an extended, harmonically distinct 20-measure “long” section. Interestingly, while Bach included a repeat symbol at the conclusion of this section, anecdotal evidence suggests some cellists opt to perform it without this second repetition. When played in this manner, the Bourrée Part I showcases a full four levels of structural scaling symmetry.
Visualizing the Structure through a Cantor Map
The Cantor set is a well-known fractal created by iteratively removing the middle third of a line segment, resulting in a structure of zero length. Its rapid disappearance can be illustrated by stacking the successive iterations, forming what is often called a Cantor comb. This term originally referred to the product of the Cantor set with an interval but has since been used more broadly.
The Cantor set can also be represented using L-systems, which are formalized rules and symbols for generating fractal structures. The substitution map A?ABA, B?BBB produces this fractal. Thus, the sections A and B need not align with the traditional “line, gap” sequence. Depending on the context, various characteristic pairs can be identified, such as “red, blue” or “loud, soft.”
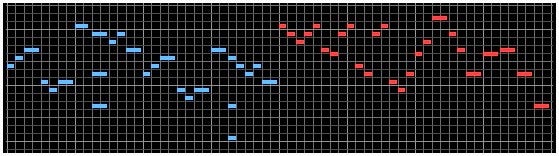
Figure 5: The Cantor comb, depicting a self-similar pattern repeating at different scales.
In this composition, the hierarchical nesting of the AAB pattern can be illustrated through a Cantor map, where each A section is itself comprised of the AAB pattern. Figure 6 shows the Cantor map for the first 16 measures of the piece.

Figure 6: Cantor map of the first 16 measures of the Bourrée Part I illustrating the nested structure of the phrasing.
In this visualization, the red areas represent four beats (two measures); blue areas signify 1 beat; and yellow areas indicate quarter beats (eighth notes). The white regions encompass everything not part of a short phrase at each scale.
This representation not only elucidates the overall structure of the piece but also highlights the relative frequencies of its components. Notably, as the length of the short phrases increases by a factor of four, their frequency diminishes by half.
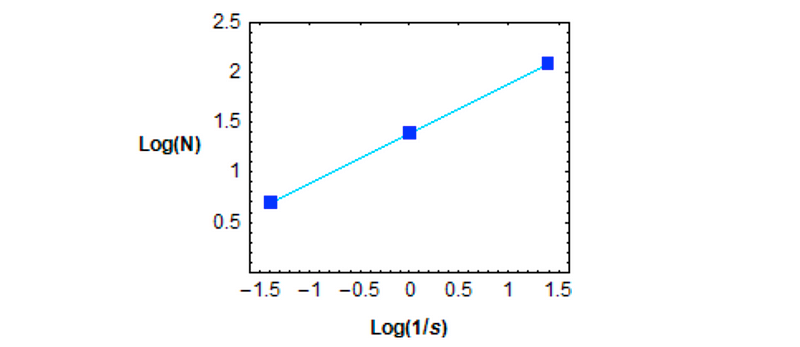
Figure 7 presents a log-log plot depicting the relationship between the count, N, and the inverse size, s (measured in beats), for the short phrases across scaling levels. The resultant straight line corroborates a power law relationship, with the slope, m, interpreted as the dimension of the object. Here, m = 1/2, a value relevant only to the phrase structure characteristics and not representing a comprehensive fractal measure for the entire composition.

Figure 7: Log-log plot of the “short phrase” count against the inverse of their respective sizes as measured in beats.
To truly appreciate the beauty of this composition, you can listen to Yo-Yo Ma's interpretation of the piece here:
Chapter 2: The Fractal Nature of Bach's Work
Bach's legacy predates George Cantor by 160 years, yet the mathematical symmetry Cantor later formalized resonates through Bach's Cello Suite No. 3. This intrinsic connection to fractal structures serves as an inspiring element for many composers in their creative processes. The evolution of the mensural canon over six centuries supports this notion, as do the fractal distributions found in the works of other classical composers and the improvisations of numerous jazz musicians.
If music reflects the composer's universe, it stands to reason that it can encapsulate the fractal essence of the world around us.
Appendix
Duration values and their symbols
The musical excerpt examined consists of quarter notes and eighth notes, where a quarter note lasts twice as long as an eighth note. Each measure contains four quarter notes (or eight eighth notes) worth of music:
Musical terminology
- Antecedent: The first of a pair of musical statements that complement each other in rhythmic symmetry and harmonic balance, similar to a rhymed couplet.
- Beat: The underlying pulse of a composition, often indicated by a conductor's movements or a metronome's click.
- Consequent: The second of a pair of musical statements that complement each other in rhythmic symmetry and harmonic balance.
- Continuation: A melodic development extending an anticipated harmonic resolution.
- Diatonic: Notes occurring naturally in a scale without modification.
- Dominant: The fifth tone of a scale, often creating anticipation resolved by returning to the tonic chord.
- Measure: A metrical division of music marked by vertical lines, containing a fixed number of beats.
- Pickup: A note or short group of notes preceding the first strong metrical beat.
- Subject: A melody or theme upon which a composition is based.
- Tonic: The note on which a scale is based; the first note of a scale.
- Transposition: Changing the key of a composition, uniformly shifting notes in a scale.
Thank you for reading! If you found this analysis engaging, feel free to hit the “Applause” icon as many times as you’d like. You can also subscribe to receive my latest content directly in your inbox.