Solution Overview

To start, let's assign the side length of the square as ( s ).

To tackle this puzzle effectively, it’s crucial to visualize the folding process. I’ll illustrate this with the following diagram.

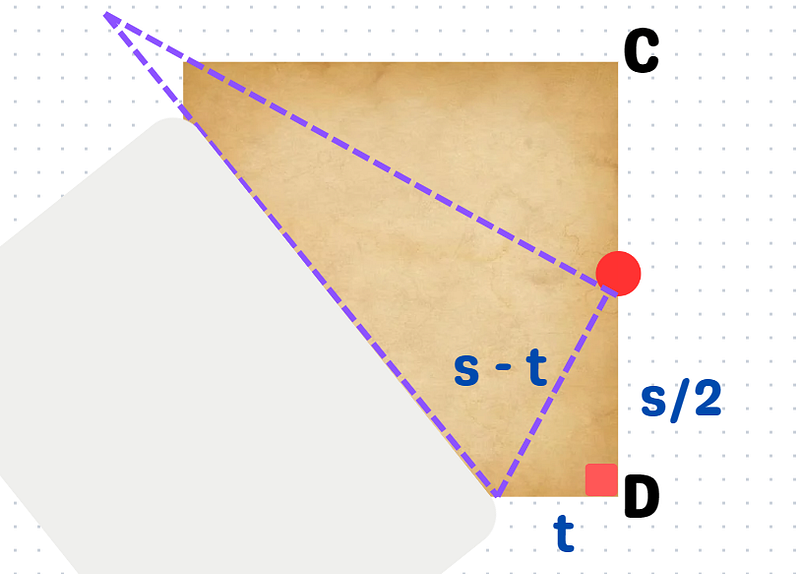
As you fold the paper, the vertex ( A ) aligns with the midpoint of ( CD ), marked by a prominent red dot. This action creates a right triangle at the base of the paper. The length of the opposite side measures ( s/2 ), which is half the length of the square.

Let’s denote the adjacent side as ( t ). Consequently, the hypotenuse will be expressed as ( s - t ). This is because the hypotenuse and the adjacent side together form the bottom edge of the square. If you’re having trouble visualizing this, I encourage you to try folding the paper yourself!

Applying the Pythagorean Theorem

Whenever we encounter a right triangle, it's beneficial to apply the Pythagorean theorem.

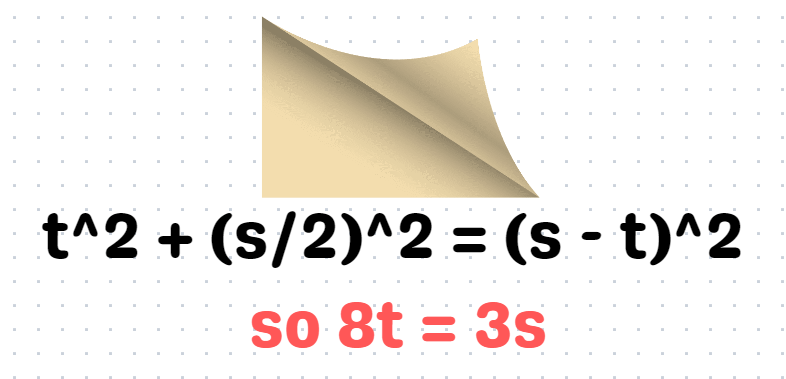
We are nearing the end of our solution. The next step is to express ( s - t ) in terms of ( s ). We can do this by substituting ( t = 3s/8 ) into ( s - t ):

[

s - t = s - frac{3s}{8} = frac{5s}{8}

]

To determine the ratio in which the crease divides ( AD ), we essentially need to find the ratio ( (s - t) : t ):

[

(s - t) : t = frac{5s}{8} : frac{3s}{8} = 5 : 3

]

Thus, the resulting ratio is either ( 5 : 3 ) or ( 3 : 5 ), depending on your perspective. And there you have it!

Reflections on the Puzzle

Isn’t it fascinating? What were your thoughts while solving this? I’d love to hear your insights in the comments below!

This video, "Origami Basics: Paper Ratios Explained - Working with Rectangles," provides a foundational understanding of how ratios function in paper folding.

Math Puzzles to Explore

If you're intrigued by this challenge, check out this collection of math puzzles on Medium, featuring topics such as Algebra, Geometry, and more!