Chapter 1: Overview of Quantum Mechanics

In traditional quantum mechanics, particles are conceptualized as waves, and vice versa. The central entity we aim to model is the wave function, which signifies the probability distribution of measurable quantities, such as position or momentum. In non-relativistic quantum mechanics, the evolution of the wave function is dictated by Schrödinger's equation, which I have discussed previously. To summarize, this equation governs the temporal evolution of a quantum state.

The limitation of this formalism is that it primarily addresses the quantum state of a single particle, like an electron confined within a box. The Schrödinger framework is suitable for such singular cases but falls short when dealing with complex physical systems that involve multiple interacting particles, such as metals or condensed matter systems. This inadequacy necessitates the adoption of more sophisticated mathematical tools to tackle these intricate systems.

Section 1.1: The Path Integral Approach

One alternative to describe a quantum system is the path integral formulation, which offers a compelling visualization of a particle's movement through space and time within a quantum framework. Here, I will not delve deeply into quantum many-body systems but will highlight the path integral concept.

In classical mechanics, we utilize a Lagrangian defined as L = T - V, where T represents kinetic energy and V signifies potential energy. From this Lagrangian, we can derive an action, S, by summing the Lagrangian over various points along the chosen path. The path that minimizes this action represents the classical trajectory of the particle.

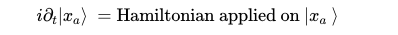
The action associated with a classical Lagrangian is expressed as an integral of the Lagrangian with respect to time, with fixed start and end points, xA and xB, at times tA and tB. To determine the classical path of a particle, we must identify the trajectory x(t) that minimizes the action.

To achieve this, we employ a technique akin to finding the minimum of a function by differentiating it and setting the derivative to zero. In this context, functional derivatives serve as the path's equivalent for identifying minimum points. We accomplish this by locating where the functional derivative of the action equals zero, leading us to the Euler-Lagrange equation.

Section 1.2: Transition to Quantum Mechanics

Now, let’s observe what occurs with a single particle transitioning from point A to point B. In quantum mechanics, particle positions are no longer characterized by straightforward coordinates as in classical mechanics. Instead, they are represented by wave functions, which I will denote below. Additionally, quantum mechanics employs 'bra-ket' notation to signify quantum states.

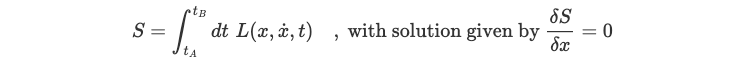
In this realm, our primary interest lies in the probability of state A transforming into state B at a specified future time. For instance, what is the likelihood that an electron's wave function appears as another wave function in 30 seconds? To formalize this, we examine the propagator, which conveys this probability.

To develop a propagator, we must achieve two objectives. First, we need a method to 'evolve' state A into the future. Once we have this evolved state, we must establish its probability of transitioning into state B. The evolution of a state is articulated through the 'evolution' operator. By applying this operator to state A and contracting the two entities, we derive the probability amplitude for the transition to state B, culminating in the formation of the propagator.

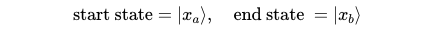
The equation below illustrates the evolution operator, denoted as U. The Hamiltonian (H) sits atop the exponential, encapsulating the quantum system's kinetic and potential energies, essential for understanding the system's evolution.

Chapter 2: The Path Integral Method

In the first video, "QFT Path Integral 1-Lecture 13 p3," the speaker discusses semi-classical expansions around various classical solutions, providing further insights into the path integral approach.

The second video, "Steve Fitzgerald - Path integral formulation of stochastic processes," elaborates on the path integral methodology in stochastic processes, further enhancing our understanding of this concept.

The final expression for the propagator is given by a somewhat complex formula, which reflects the nuances of quantum behavior. This diagram visually represents the path integral used to calculate the probability of transitioning from state A to state B over time. A particle can traverse various intermediate states between these two points, as depicted along the pink line.

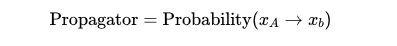
Thus, the pink line exemplifies one potential trajectory a particle may follow from A to B, each with an associated probability known as a phase. The path integral itself sums the probabilities of all conceivable paths, mathematically termed a path integral.

The G on the left side of this equation represents the conventional notation for the propagator, while the capital D signifies the integral across all paths. Remarkably, the phase factor—the probability that a particle follows a specific path—is expressed as the exponent of the Lagrangian multiplied by the imaginary unit i. Consequently, L symbolizes the Lagrangian multiplied by i.

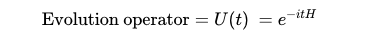
In general, we should not anticipate significant quantum corrections to classical principles. After all, Newton's classical laws of motion remain effective; thus, why do we not observe drastic changes in our everyday experiences? This phenomenon is largely attributed to the cancellation of many paths. Near a classical trajectory, numerous phase factors are similar, leading to constructive interference that accentuates the classical path as the predominant term in the integral.

To illustrate this point, we will demonstrate that paths close to the classical trajectory share a similar phase, enabling them to constructively interfere with each other. Though this explanation may seem vague, it serves as an introductory concept.