Data and Methodology

The data is sourced from Basketball Reference. The model is trained using 1,300 rookie seasons from the "3-point era," starting from the 1979/80 season. Each season included must have featured at least 30 games played and an average of 7 minutes per game. The final rookie season included in the analysis is 2010/11, as players debuting afterward may still have opportunities to become All-Stars. Out of the 1,300 rookies, 197 eventually made at least one All-Star appearance.

For the analysis, I utilized R along with the randomForest and ROCR packages, and all relevant data and code can be found on my GitHub repository.

Constructing the Model

I employed a Random Forest Classifier for this analysis. This method is versatile, leveraging multiple decision trees to categorize observations. Each tree uses a randomly selected set of predictive features. The final classification is determined by the majority vote from all decision trees.

The model incorporates 13 distinct features:

• Minutes played per game
• Points scored per game
• Offensive rebounds per game
• Defensive rebounds per game
• Blocks per game
• Steals per game
• Assists per game
• Effective field goal percentage (normalized for the league average)
• Free throw percentage
• Age
• Offensive Box Plus Minus (OBPM)
• Defensive Box Plus Minus (DBPM)
• Usage rate
• Turnover rate

Fine-Tuning the Model

Initially, I fitted the model using 750 decision trees and then optimized it to enhance performance. The hyperparameter I focused on is the number of features per tree, denoted as m???, aiming to reduce the out-of-bag (OOB) error. The optimal value for my dataset turned out to be 4.

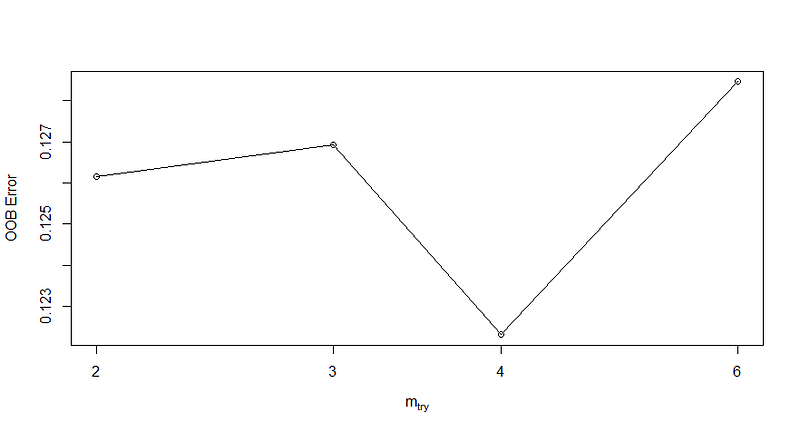
With m??? set to 4, the model exhibits an OOB estimated error rate of 12.54%, suggesting that it is likely to misclassify about 12.54% of the time.

We can further observe how the error rate fluctuates with an increase in the number of trees:

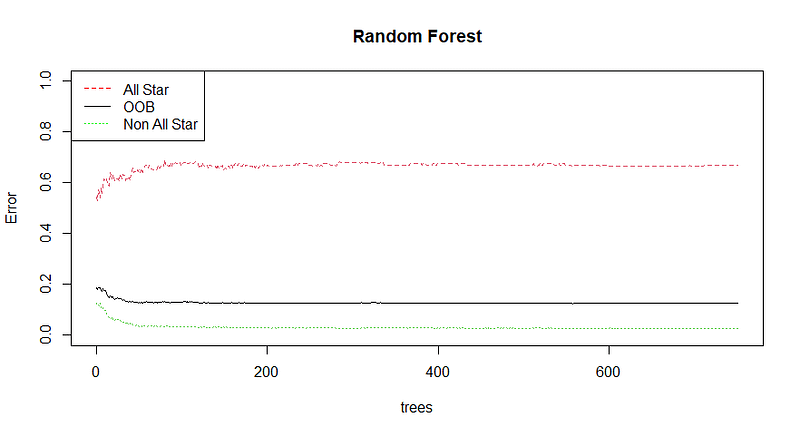
Initially, increasing the number of trees diminishes the OOB error, but it plateaus just above 12%. Thus, 750 trees suffice to reach the model's full potential.

The confusion matrix below illustrates the model's classification accuracy compared to actual results:

As expected, the model misclassifies a significant portion of All-Stars, missing about two-thirds of them.

Feature Importance Analysis

The charts below highlight the importance of each feature in making classifications. The left chart indicates how accuracy declines if a feature is omitted, while the right chart measures the reduction in Gini impurity. Features at the top are deemed most critical, while those at the bottom are the least impactful.

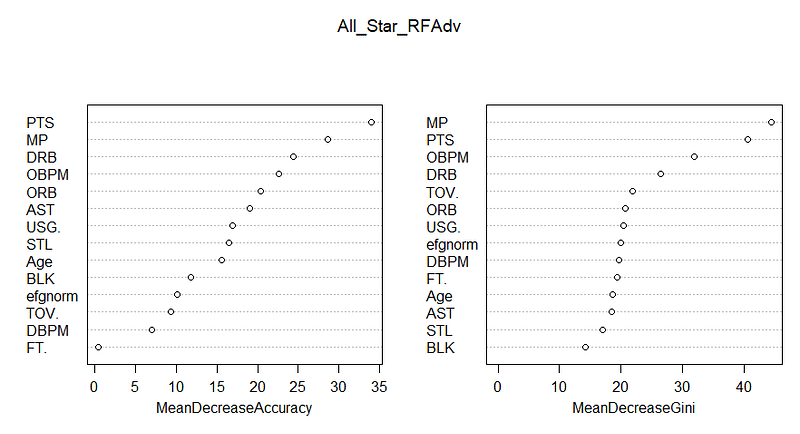
The standout metrics include minutes played and points per game. Interestingly, defensive rebounds (DRB) play a larger role than expected. In contrast, effective field goal percentage and free throw percentage can be excluded with minimal loss in accuracy, suggesting high correlation between the two.

The analysis indicates that offensive metrics, represented by OBPM, are more significant than defensive ones, as shown in both charts. However, quantifying defensive contributions remains challenging, and while advanced tracking stats have improved our understanding, they aren't yet widely applicable for this model.

Evaluating the Model's Performance

The Receiver Operating Characteristic (ROC) curve below illustrates how the false positive rate varies with different discrimination thresholds. By default, the threshold is set to 0.5, which can be adjusted, but I find the default adequate.

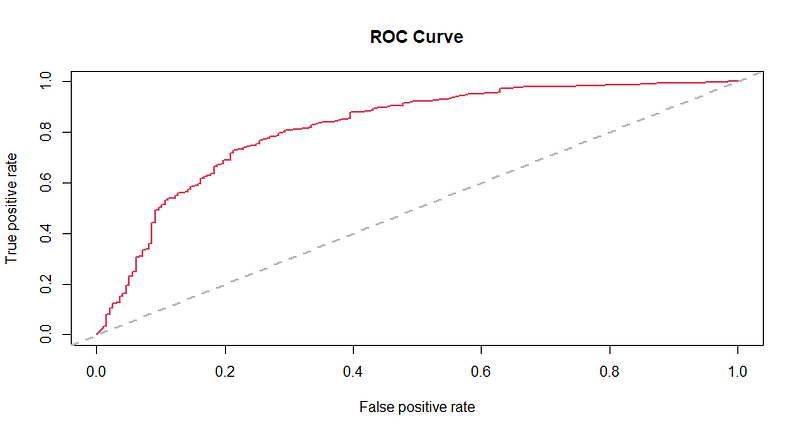
The area under the ROC curve (AUC) is a crucial metric for assessing model efficacy. It ranges from 0.5 (indicating random guessing) to 1 (indicating perfect discrimination). This model achieves an AUC of 0.818, which is commendable.

To enhance the model further, integrating advanced player tracking data could be beneficial. However, since this data is only available from the 2013/14 season onward, it is not feasible for training a model at this stage. Another potential improvement could involve factoring in team strength, as promising players on strong teams might have less playing time compared to those on weaker teams.

Insights from the Model

Earlier, I questioned if the model could differentiate between the rookie seasons of Evan Turner and Paul George. Ultimately, it assigned Paul George a 33% probability of becoming an All-Star, while Evan Turner received only a 7.5% chance. Though both were categorized as non-All-Stars, the model effectively recognized a meaningful distinction between the two.

Among the training sample players, the model forecasted the highest likelihood for Tim Duncan—over 96% chance of All-Star status, which aligns with his rookie season achievement. High probabilities were also noted for Shaquille O’Neal (94.3%) and Pau Gasol (93.3%).

Conversely, Clark Kellogg was flagged as a false positive with nearly a 90% chance of being an All-Star, despite knee injuries that curtailed his career after five seasons. On the flip side, Jayson Williams and Ricky Pierce received 0% odds from the model, yet both made it to one All-Star game.

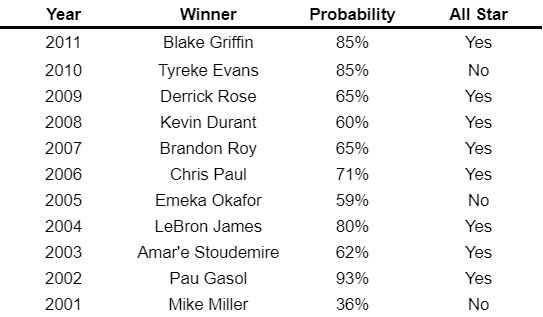
The model's performance with Rookie of the Year winners is summarized below:

Future Predictions for the 2020 Draft Class

Using the model, I can project outcomes for the 2020 draft class. If re-drafted based on this model’s predictions (excluding some players with limited data), the results would be as follows:

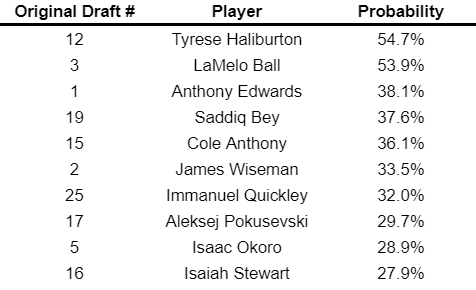
While no standout prospects emerged, the model predicts that two potential All-Stars—Tyrese Haliburton and LaMelo Ball—could arise from this group. The confusion matrix results suggest that there may be additional hidden talents among the less remarkable rookies.