How Aristarchus Determined the Moon's Size: A Deep Dive
Written on
Chapter 1: Introduction to Aristarchus
In our previous exploration, we traced the methods of Aristarchus as he measured the Earth's circumference. Today, we will continue our quest for knowledge by investigating how he assessed the size of one of our closest celestial neighbors: the Moon.
When we gaze up at the night sky, the Moon captivates us, yet its size remains a mystery. Despite the common knowledge that the Sun is significantly larger and farther away than the Moon, this understanding is not innate. Notably, during a solar eclipse, the Moon obscures the Sun, revealing its proximity. This observation indicates that the Moon is indeed our nearest celestial body.
The angular dimensions of the Sun and Moon are strikingly similar, suggesting that while the Sun is larger, their apparent sizes from our perspective align closely.
Aristarchus postulated that during a lunar eclipse—when the Earth is positioned between the Sun and the Moon—the latter disappears into the Earth's shadow for approximately two hours. He theorized that this loss of visibility occurs because sunlight is blocked by the Earth, which reflects his understanding that the Moon shines by reflecting sunlight.
Section 1.1: The Mechanics of Lunar Eclipses
Aristarchus began his analysis by calculating the ratio of the angular size of the Earth's shadow to that of the Moon. He determined the Earth's shadow size by observing the Moon just before and after it entered the shadow. He believed the Moon's orbit was circular, making it feasible to measure its size during a Full Moon. This led him to conclude that the ratio of their angular sizes would correlate directly with their physical sizes—specifically, a ratio of about 2.5.
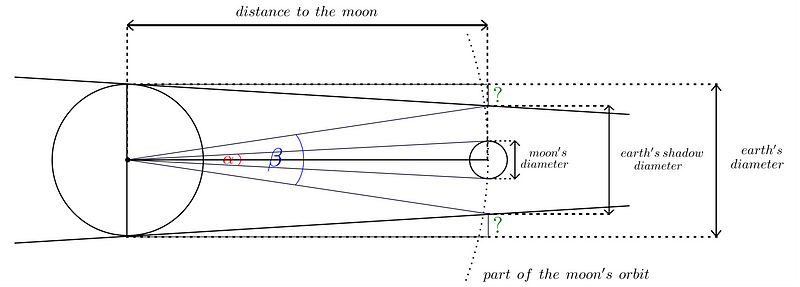
The only known measurement for Aristarchus was the Earth's diameter, established earlier by Eratosthenes. By using the dimensions derived from the Earth's shadow and the Moon's diameter, he could compute the Earth's size based on the proportions he had established.
However, the equations involved contained unknown variables. To solve this, he introduced the Sun into his calculations, as its angular size matched that of the Moon.
Section 1.2: The Role of Geometry
Aristarchus recognized that by visualizing a triangle formed by the Earth, Moon, and Sun, the angles would sum to 180 degrees, and he could identify a common angle.
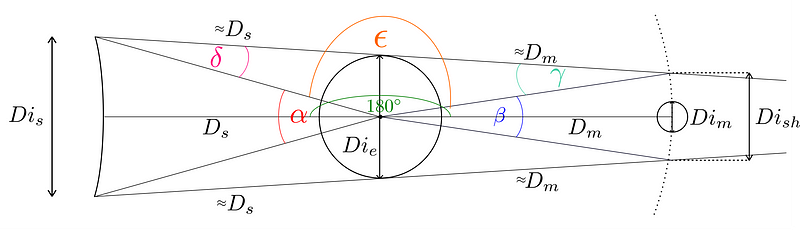
He labeled the angular size of the Sun as ?—a value equal to that of the Moon. By substituting this into his equations, he could derive a relationship between the various celestial dimensions.
Substituting values allowed him to refine his calculations. By applying the tangent formula to the triangle's relationships, he could establish connections between the distances and sizes of the Earth, Moon, and Sun.
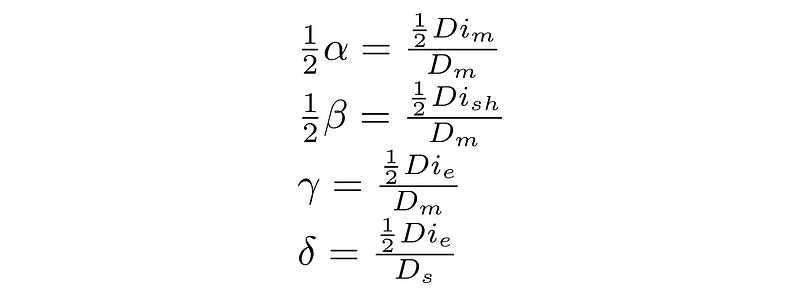
Aristarchus estimated the Sun's distance to be approximately 20 times that of the Moon, disregarding factors that were negligible in his calculations.
After a series of calculations, he concluded that to determine the Earth's diameter from the shadow measurement, one must add the Moon's diameter.
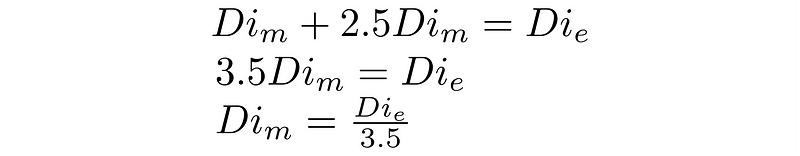
Ultimately, Aristarchus's estimations indicated that his approximations were quite astute, as he approached the true value of the Moon's size.
Chapter 2: Video Insights
This video titled "Measuring the Size and the Distance of the Moon by Aristarchus" delves into the methodology used by Aristarchus and the historical context of his findings.
In this video, "Astronomy - Measuring Distance, Size, and Luminosity (3 of 30) The Size of the Moon," viewers can learn more about how astronomers measure the Moon's size and its significance in the broader scope of astronomy.