Exploring a New Equation for Gravity: Insights from Astrophysics
Written on
Chapter 1: Scientific Method in Cosmology
The scientific method is fundamentally about proposing and rigorously testing hypotheses. Previous discussions have introduced various hypotheses concerning events preceding the Big Bang. Testing these ideas is often challenging, if not unfeasible. An indirect method of validation involves inferring what these hypotheses might suggest about our universe. Given that multiple hypotheses can lead to similar conclusions, it becomes impossible to definitively prove any single hypothesis. However, if the tests yield statistically insignificant results, one might reasonably conclude that the principal hypothesis lacks substantial support.
Section 1.1: Velocity Anomalies in Stellar Motion
In the preceding article (#26 - Does Dark Matter Exist?), we examined the possibility that Newton's inverse square law of gravity requires modification. To investigate these modifications, we can predict the velocities of stars and galaxies within clusters. For nearly a century, scientists have observed that many stars exhibit velocities that exceed those anticipated by Newton’s laws. This discrepancy has led to the introduction of dark matter as a potential explanation, though its true nature remains elusive.
A suggested revision to Newton’s gravitational law incorporates various factors, including the ages of galaxies and stars, their initial and current temperatures, and the distances of stars from the galaxy's center at both points in time. Much of this information is not easily accessible. Drawing from Professor Susskind’s theories regarding black holes, a new equation has emerged for calculating gravitational force over small time increments:
Fg = KC ~ {4 * m? * m? * (A? / A?) * (T?? / T??)} / (G² * {[d? * (T?? / T??)] + d?}²)
where:
Fg = Gravitational force;
KC = Kolmogorov Complexity;
G = Gravitational constant;
A? = Age of the galaxy;
A? = Age of the star;
d? = Distance from the star to the galaxy's center at birth;
d? = Current distance;
m? = Mass of the galaxy at radius d?;
m? = Mass of the star;
T?? = Star's temperature at birth;
T?? = Star's current temperature.
Under conditions where A? = A?, T?? = T??, and d? = d?, this equation simplifies to Newton’s law.
The video titled "Cavendish Gravity Experiment: Setting up the math to calculate G" provides foundational insights into gravitational calculations.
Section 1.2: Centripetal Acceleration and Stellar Velocities
According to Newton’s Second Law of Motion, the relationship between force, mass, and acceleration is defined as:
Force = mass * acceleration.
For a mass orbiting another, the gravitational force translates to centripetal acceleration, expressed as:
Centripetal acceleration = mass * v?² / distance from the galaxy's center.
In this equation, v? denotes the star's velocity. Rearranging this allows us to predict stellar velocity by substituting our gravitational force equation, Fg, for centripetal acceleration, yielding:
v?² = {4 * m? * (A? / A?) * d? * (T?? / T??)} / (G² * {[d? * (T?? / T??)] + d?}²).
Assuming no information about a star's birth temperature, we can simplify it to:
v?² = {4 * m? * (A? / A?) * d?} / (G² * {d? + d?}²).
Another simplification assumes that differences in distances d? and d? stem solely from the expansion of space (dark energy).
Chapter 2: Galaxy Rotation Curves and Observational Data
Astrophysicists are continuously advancing techniques to measure stellar velocities around a galaxy's center. Findings indicate that many stars move significantly faster than predictions based on Newton’s Second Law. Two primary explanations have emerged: (i) the presence of invisible mass, termed dark matter, which does not emit light, and (ii) Modified Newtonian Dynamics (MOND), which alters Newton's gravitational equations based on observational data rather than theoretical derivations.
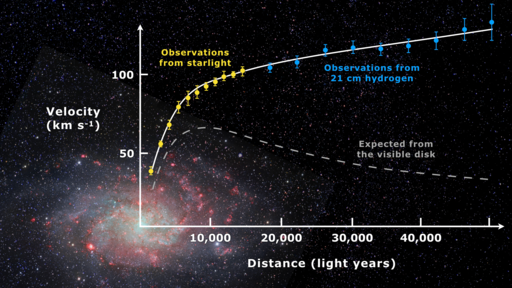
Astronomical consensus holds that galaxy rotation curves exhibit (i) an increase near the galactic center and (ii) a relatively flat profile, contrary to Newtonian predictions. For instance, observations of the Messier 33 galaxy illustrate this divergence. The curve labeled ‘Expected from visible disk’ reflects predictions based on Newtonian gravity, while actual measurements reveal discrepancies.
The next article will leverage data from a database of 175 galaxies to compare predicted stellar velocities using both Newtonian laws and the newly proposed formula. However, limitations exist, as the SPARC database lacks comprehensive details on star ages and temperatures. Moreover, the current equation does not differentiate between masses that convey information and those that do not. Therefore, a revised formula is applied.
The foundational formula (excluding the gravitational constant) is:
v?² ~ {(m? + m? + m?) + [(m? * k?) * (1 + k?)]} / d?
where:
v? = star velocity,
m? = mass of stars in the bulge within radius d?,
m? = mass of stars in the galaxy's disk within radius d?,
m? = mass of gas within the galaxy,
d? = distance from the center of the galaxy,
k? = adjustment factor based on average star age and temperature,
k? = adjustment factor reflecting the average increase in distance due to spatial expansion.
The SPARC database includes velocity estimates for various mass types: bulge, disk, and gas. The mass within a given radius is determined by calculating the square root of the sum of squares of velocities across these mass types.
The first term in the velocity equation (m? + m? + m?) aligns with Newtonian mass, representing Lloyd’s nodes in space. The second term (mg * k?) approximates the number of links, while the third term, k?, quantifies the growth in link length. For a galaxy aged 13.8 billion years, k? is approximately 1.02. Further discussion on the age and temperature-dependent adjustment factor k? will follow in the next article.
When comparing root mean square errors (RMSE) for velocity predictions, the gravitational constant can be omitted without affecting conclusions about the equations' predictive capabilities. Notably, the modified equation reduces the RMSE for galaxy velocity predictions from -19% using Newton's equation to -0.04% when k? equals 2.7. When further adjustments are made as discussed in Article 24 - Rethinking Dark Matter, the RMSE aligns with that of Newton’s unmodified equation, suggesting that this revised equation could elucidate the observed rotation curves of galaxies.
In a subsequent article, we will analyze actual data for our sun, demonstrating that its velocity predictions align with the Kolmogorov equation when the galaxy's mass is adjusted by a factor of 4.5, remarkably close to the average dark matter to matter ratio of 5.7 in our universe. For Earth, applying the Kolmogorov equation to account for a threefold rise in temperature since its formation suggests that this temperature increase effectively counters the potential influence of dark energy on gravity over Earth's lifespan.
In conclusion, this article raises a pivotal question:
Should Newton’s law of gravity be superseded by a theory that accounts for how information influences the very structure of space-time?