Chapter 1: The Essence of the Theorem

The Fundamental Theorem of Arithmetic asserts that any positive integer greater than one is either a prime number or can be expressed as a product of prime numbers. Notably, this factorization is unique aside from the order in which the factors are arranged. These principles are pivotal in mathematics, deserving the title of the fundamental theorem of arithmetic.

To validate this theorem, two distinct proofs are required. The first proof establishes that every integer greater than one that isn't prime can be expressed as a product of primes. The second proof confirms the uniqueness of such prime factorizations.

It's essential to clarify that the integer 1 is not classified as a prime number, which is why it cannot serve as a factor in any prime product. This exclusion will become clearer as we progress. For our current discussion, it's sufficient to recognize that in the context of the fundamental theorem, 1 is treated as an empty product—one that arises from multiplying no factors at all.

The Well-Ordering Principle and the Initial Proof

We begin our first proof utilizing the well-ordering principle, which states that every non-empty subset of non-negative integers has a least element. For instance, consider the set of integers greater than one:

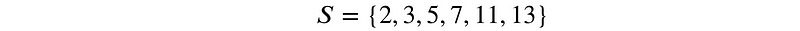
This set meets the criteria of the principle: it is non-empty and consists of non-negative integers. The least element here is 2.

Now, let's move on to the proof itself, which operates via contradiction. We assume the opposite of what we aim to prove: that there exists a positive integer greater than one that cannot be expressed as a product of primes. By the well-ordering principle, this integer must be the smallest, which we denote as n.

If n is a prime number, our proof is complete. However, if n is composite, it can be broken down into factors that are all smaller than n and greater than one. Each of these factors, being smaller than n, can be represented as a product of primes. Therefore, n, being composed of primes, must also be expressible as such—a contradiction to our original assumption. For example, consider 210, which can be factored into 14 and 15. Both of these can be further broken down into primes, demonstrating that 210 can indeed be expressed as a product of primes: ( 2 times 3 times 5 times 7 ).

This contradiction implies that no composite number can exist that isn’t expressible as a product of primes.

Euclid’s Lemma and the Second Proof

The second part of the theorem, which asserts that the factorization of every positive integer greater than one is unique, relies on Euclid’s lemma. This lemma states that if a prime p divides the product of two integers a and b, then p must divide at least one of those integers.

For instance, let’s take p = 7 and consider the product ( 21 times 23 = 483 ). Since 7 divides 483, it must divide 21 or 23. It's straightforward to verify that 7 divides 21 (7 × 3 = 21).

Euclid’s lemma leads to two significant corollaries: one extends the lemma’s applicability to products with more than two factors, while the other states that if a prime divides a product of primes, it is equal to one of those prime factors.

Returning to the fundamental theorem, we aim to prove that every positive integer greater than one has a unique prime factorization. For this proof, we again use contradiction. Assume that a positive integer n has two distinct factorizations:

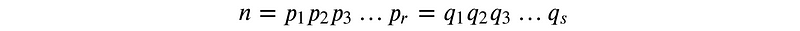
Assuming both factorizations consist of prime factors, we arrange them in ascending order.

The smallest prime factor in one factorization must divide n, and thus also divides the product of the other factorization. According to the second corollary of Euclid’s lemma, this smallest prime factor must match one of the primes from the other factorization, leading to a contradiction.

Continuing this reasoning, we would arrive at the conclusion that all prime factors must be identical, proving that any positive integer greater than one can only be factored into primes in a unique way.

Understanding Why 1 Is Not Prime

Finally, we can comprehend why the integer 1 is excluded from being classified as a prime number and considered an empty product. The fundamental theorem of arithmetic claims that every positive integer greater than one has a unique set of prime factors. If 1 were included as a factor, this uniqueness would be compromised.

1 acts as the multiplicative identity; multiplying by 1 does not change a number. Therefore, any number could have numerous factorizations involving 1, which would contradict the theorem's assertion of uniqueness. For instance, consider the factorizations of 48:

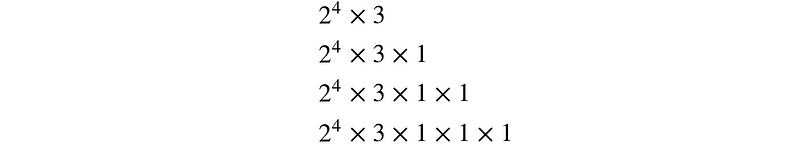
To maintain the integrity of unique factorizations for integers greater than one, we must exclude 1 from the set of prime numbers.

Chapter 2: Video Insights

This video titled "The Fundamental Theorem of Arithmetic" offers a detailed explanation of the theorem, its proofs, and its implications in mathematics.

In this video, "The Fundamental Theorem of Arithmetic," viewers can explore the significance of prime factorization and its role in number theory.