What Happens If Your Cat Leaps Through the Earth's Core?
Written on
Chapter 1: The Cat's Curious Journey
Cats are known for their adventurous spirits, and if your feline companion were to discover a tunnel leading through the Earth's core, it's likely she wouldn't hesitate to leap right in. As she plunges down, her speed would increase until she reaches the center, and then she would continue to ascend to the other side of the planet. But how long would this journey take?
When this scenario unfolds, you might want to have a catnip-filled toy ready. If your aim is precise and conditions are ideal—meaning no air resistance—you could toss the toy mouse into orbit around the Earth just as your cat jumps in. If executed correctly, both the cat and the mouse should arrive at the tunnel's exit simultaneously.
As humorously noted in Douglas Adams' "The Hitchhiker's Guide to the Galaxy," mastering flight is essentially about learning how to fall and miss the ground. The Moon and Earth are in a perpetual dance of falling toward each other while evading collision. The moment you release the toy mouse, a gravitational force pulls it towards the Earth's center.
Section 1.1: The Physics of Falling
How long does it take for the toy mouse to travel from one pole of the Earth to the other? The centripetal acceleration of the mouse must equal the force of gravity acting upon it.

To calculate this, we consider the Earth's radius of approximately 6,400 km to determine the orbital velocity.
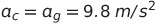
Before diving into numbers, it's important to note that we're interested in the orbital period T. The path taken will be along the circumference, C, and the ½ subscripts indicate that we are measuring the time it takes to orbit halfway around the Earth.
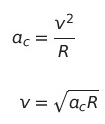
The result? It takes about 42 minutes for the mouse to complete its journey. The mass of the mouse, whether it's 1 gram or 1 kilogram, is irrelevant, so feel free to fill it with catnip!
Section 1.2: The Cat's Motion
Interestingly, your cat's trajectory through the Earth mirrors that of the mouse. She would reach the South Pole just in time to catch her toy. If she chooses, she can oscillate back and forth like a spring. At the Earth's center, her speed would peak, matching the orbital velocity of the mouse. She would then decelerate and reverse direction at the poles.
What if we were to create a shorter tunnel that exits at the same location? If we drop the mouse into this shorter tunnel just as the cat enters the longer one, we'd need to consider a few assumptions. For the sake of this thought experiment, we will assume the Earth is uniform, disregard friction between the mouse and the tunnel walls, and ignore any cat's natural aversion to hot magma. Treat your cats like the celestial beings they are!
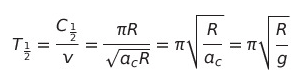
Now, let’s explore the two parallel paths through the Earth.

Both the cat and mouse experience equal magnitudes of acceleration directed towards the Earth's center. However, only the cat feels the full force of this acceleration, while the mouse only experiences a reduced effective acceleration.
If we define this adjustment factor as ?, then the oscillation periods for both the cat and the mouse will remain consistent across various tunnel lengths.
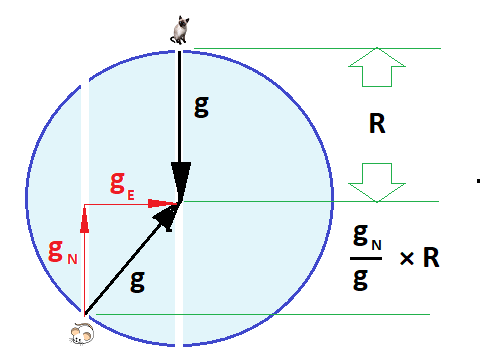
No matter the length of the tunnel, the answer in minutes will consistently be 42.