Understanding the Benefits of Braess's Paradox in Traffic Dynamics
Written on
Chapter 1: Introduction to Braess's Paradox
Braess's Paradox reveals a surprising phenomenon in traffic networks where adding roads can reduce overall efficiency. This concept was introduced by Dietrich Braess, a mathematician from Ruhr University, Germany, during his 1968 research on traffic flow modeling. Initially, the idea seems illogical—how could more roads lead to slower traffic? This article will delve into the paradox through mathematical analysis, real-world applications, and its implications beyond transportation.
Section 1.1: Setting Up the Model
To illustrate Braess's Paradox, we will create a hypothetical road network. Imagine a scenario where 1000 vehicles must travel from a location labeled 'START' to another called 'END.' There are two routes available: one through junction 'A' (START-A-END) and another through junction 'B' (START-B-END).
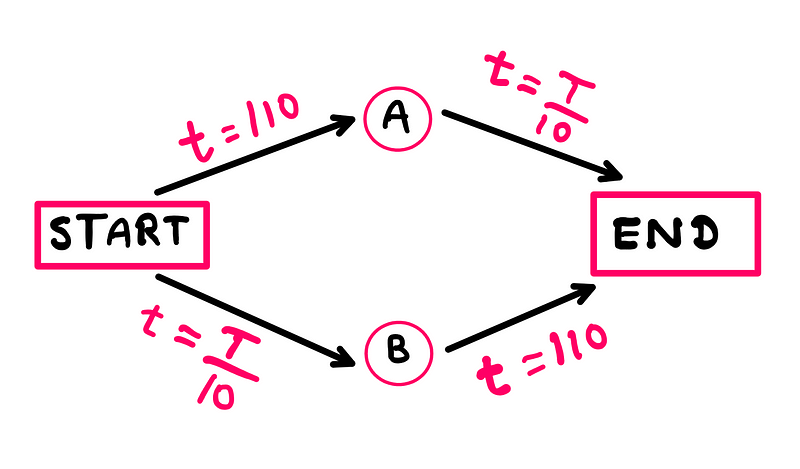
For the first route, the travel time from 'START' to 'A' (START-A) is fixed at 110 minutes, while the time from 'A' to 'END' (A-END) depends on traffic flow, represented mathematically as (T/10) minutes, where 'T' indicates the number of cars on the A-END route. Conversely, for the route through 'B,' the time from 'START' to 'B' (START-B) varies based on traffic (T/10), but the time from 'B' to 'END' (B-END) is constant at 110 minutes.
Section 1.2: Analyzing the Mathematics
Next, we will analyze how this network functions mathematically. The travel time for vehicles using the START-A-END route can be expressed as follows:
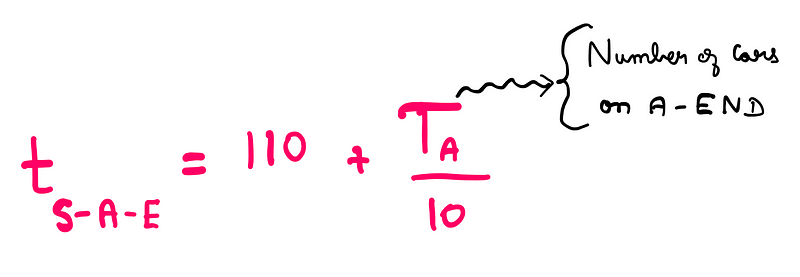
The formula for vehicles traveling via the START-B-END route is similarly constructed:
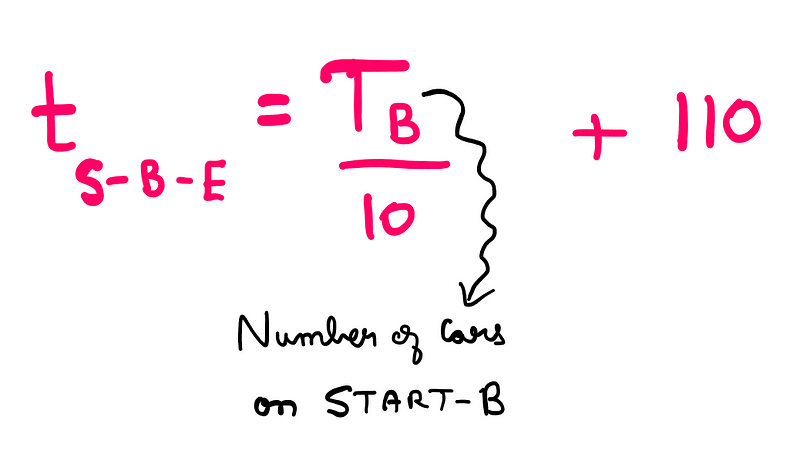
If we assume the system reaches a Nash equilibrium, half of the vehicles will take each route, resulting in equal travel times of 160 minutes.
Chapter 2: Introducing a New Road
Now, let's add a new route that connects junctions 'A' and 'B' (A-B), which we assume can be traversed in 0 minutes. This addition allows drivers to switch paths at their discretion.
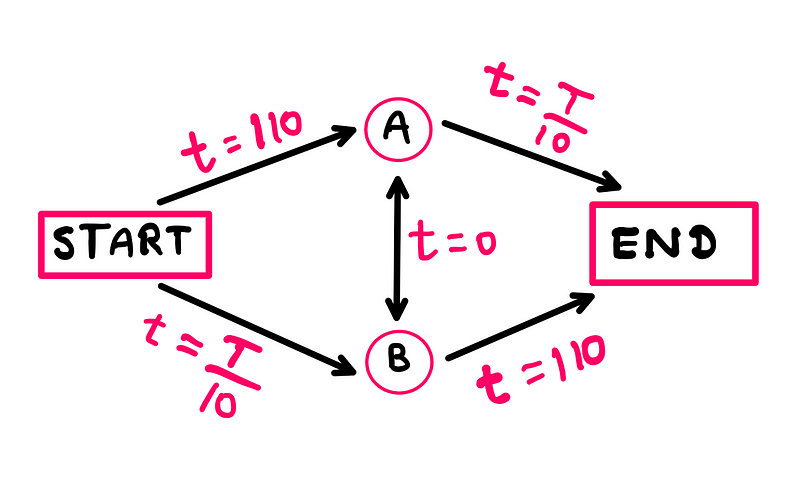
Starting from our previous equilibrium, if a driver opts for the START-B-A-END path, they may find a significantly shorter travel time. This choice prompts more drivers to consider the new route, gradually increasing the traffic on it.
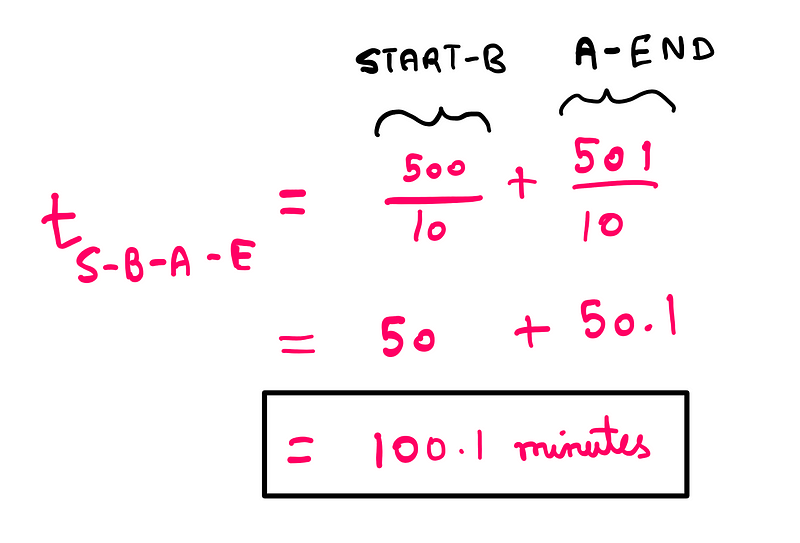
As more vehicles choose this route, the travel time increases until it balances out. Once 600 vehicles take the new route, the previously realized time advantage disappears, leading to a new equilibrium.
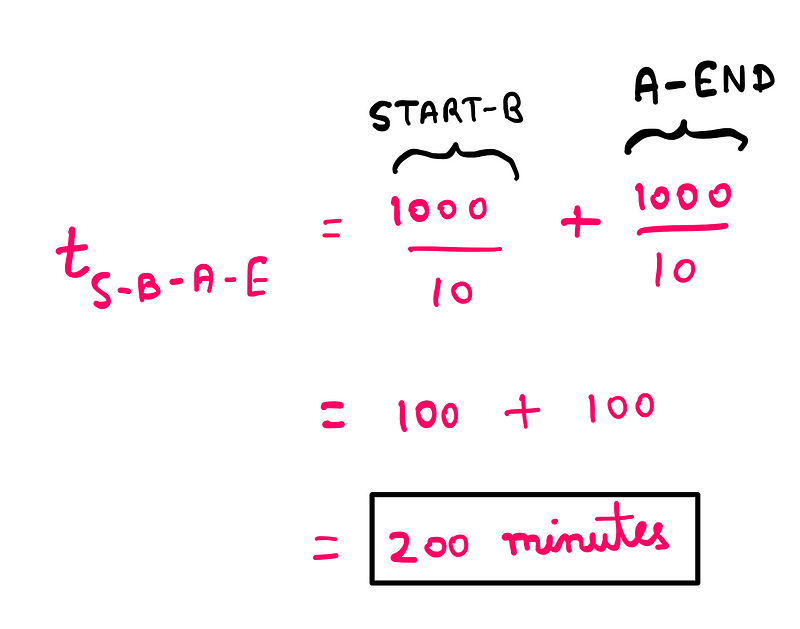
Ultimately, the introduction of the new road (A-B) results in longer travel times for all drivers compared to the original configuration, highlighting that Nash equilibrium does not necessarily equate to the shortest travel time.
The first video, "Braess's Paradox - Equilibria Gone Wild," offers an engaging exploration of this paradox's dynamics and implications.
Section 2.1: Practical Applications
Braess's Paradox has real-world implications. Research by Gastner et al. in 2008 showcased that closing certain roads in cities like Boston, New York, and London improved traffic flow. Following this, New York City shut down sections of Broadway in 2009, leading to enhanced traffic conditions and the establishment of permanent pedestrian plazas.
In 2012, a bridge fire in Rouen, France, provided another example; the subsequent detour improved traffic flow, as fewer vehicles crossed the remaining bridges.
The concept extends to fields beyond transportation. For instance, in electrical grids, excess capacity can hinder power delivery speeds, mirroring the road network scenario. Motter et al. demonstrated similar effects in ecological systems, where the removal of a detrimental species can stabilize the ecosystem.
The second video, "How Closing Roads Could Speed Up Traffic," further elaborates on the paradox and its implications for urban planning.
Final Thoughts
Braess's Paradox exemplifies how an intriguing mathematical observation can yield significant insights across multiple domains. However, practical applications require careful consideration, as real-world networks are complex and sensitive to changes. Utilizing mathematical modeling can help dynamically manage networks, ensuring optimal flow and efficiency.
For further reading, consider exploring related topics such as "How To Solve The Three 3s Problem?" and "How To Really Use Mathematical Induction?"